A: Raumbezogene Datenanalysen
Aus Sicht der den Geo-Informationssystemen zu Grunde liegenden Datenbanksysteme lassen sich Analysefunktionen ganz generell in Standard- und Nicht-Standardanalysen unterscheiden. Dabei sind mit Standardanalysemethoden die Methoden gemeint, die sich mittels der in relationalen Datenbanksystemen verfügbaren und aus der relationalen Algebra abgeleiteten Anfragen realisieren lassen. Zu diesen Operationen gehören etwa Selektionen von Werten, die bestimmte Bedingungen erfüllen, logische Verknüpfungen mittels Boolescher Algebra, Sortierungen oder Gruppierungen von Datenreihen oder die Ableitung einfacher statistischer Kenngrößen, die üblicherweise bereits mittels der Abfragesprache SQL (Structured Query Language) auf relationalen Datenbanken formuliert werden können. Abfragen und Analysen hingegen, die spezielle geometrische, topologische oder temporale Operationen benötigen, gehören zu den Nicht-Standardanalysen und machen entsprechende Systeme wie GIS erforderlich. Wie vorher beschrieben sind heute bereits ausgewählte geometrisch-topologische Funktionen in objektrelationalen Datenbanken enthalten, sofern diese um räumliche Datentypen und Operatoren erweitert sind, z. B. in Microsoft SQL Server, Oracle Spatial, MySQL oder PostgreSQL (PostGIS). PostGIS als räumliche Erweiterung für PostgreSQL bietet z. B. räumliche Datentypen wie Polygone, Linienzüge und Punkte, räumliche Operatoren zum Vergleich von Geometrien bzgl. Überlappung und räumliche Funktionen wie Flächen- und Abstandsberechnungen, Flächenverschneidungen, Pufferbildungen oder Koordinatentransformationen.
Die Datenanalyse ist das Herzstück eines GIS. Hierzu gehören Funktionen wie die Flächenverschneidung, die Netzwerkanalyse, digitale Geländeanalysen, Berichtsgenerierungen, statistische Analysen sowie sehr viele aus den Anwendungsanforderungen abgeleitete spezielle Funktionen, die vermehrt auch bereitgestellt werden. So können zum Beispiel die Informationen bereitgestellt werden, um mittels der kürzesten Wegeberechnung Fahrzeugfahrer über die an Bord befindlichen Fahrzeugnavigationssysteme gezielt von einem Startpunkt zu einem Zielpunkt zu führen.
Gruppierung und Auswahl gängiger GIS-Analysemethoden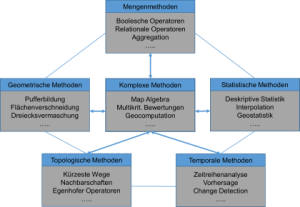
Analysemethoden lassen sich grob in 6 Gruppen einteilen (zu den Funktionalitäten und Methoden vergleiche Bill, 2016, Kapitel 7 resp. de Smith et. al. 2018):
- Geometrische Methoden beruhen im Wesentlichen auf mathematischen Grundlagen der Geometrie. Sie sind durch das Rechnen mit Koordinaten ausgezeichnet. Wichtige Funktionen sind die Abstands- und Flächenberechnung (z. B. für Flurstücke einer Kommune), die Zonengenerierung (z. B. um eine geplante Trasse), die im Video erklärte Punkt-im-Polygon-Prüfung (z. B. Messstellen in einem Ortsteil), die nachfolgend animiert erläuterte Flächenverschneidung (z. B. Flurstücke mit Realnutzung) und die Dreiecksvermaschung (z. B. Digitale Geländemodelle).
Point-in-PolygonFlächenverschneidung - Topologische Methoden bauen auf Nachbarschaftsbeziehungen auf; sie nutzen im Wesentlichen die Graphentheorie als mathematische Grundlage. Mit ihnen lassen sich Nachbarschaftsbeziehungen (zwei Flurstücke grenzen aneinander) ohne Nutzung von Koordinaten ausdrücken. Bekannte Funktion ist die Berechnung der kürzesten Wege in einem Netz (z. B. einem Leitungsnetz).
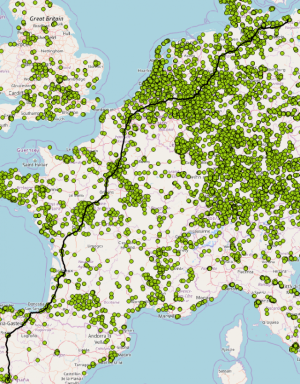
Kürzester Weg vo Rostock nach Madrid (eine Übungsuafgabe zur Elektromobilität).
- Mengenmethoden setzen auf der Booleschen und relationalen Algebra auf. Sie dienen der Eingrenzung selektiver Abfragen auf dem Datenbestand (z. B. alle Flurstücke größer als 1.000qm und zur Bebauung geeignet). Typische Funktionen sind aber auch die Sortierung von Daten (z. B. der Größe oder dem Alphabet nach) zur Listenausgabe. Eine komplexere Methode ist die Aggregation, illustriert im folgenden Video.
Aggregation - Statistische Methoden sind in der Wahrscheinlichkeitstheorie und Stochastik begründet. Die angebotenen Funktionen reichen von der einfachen beschreibenden Statistik (z. B. mittlere Größe der Flurstücke im Gemeindegebiet) über die induktive Statistik bis hin zur Geostatistik (z. B. Interpolation von Grundwasserständen in einer Gemeinde mittels Kriging).
Boxploterstellung - Temporale Methoden gestatten raum-zeitliche Auswertungen. Dies reicht von einfachen Zeitoperationen in selektiven Abfragen (vorher-nachher) bis zu Interpolationen oder Extrapolationen sowie Zeitreihenanalysen.
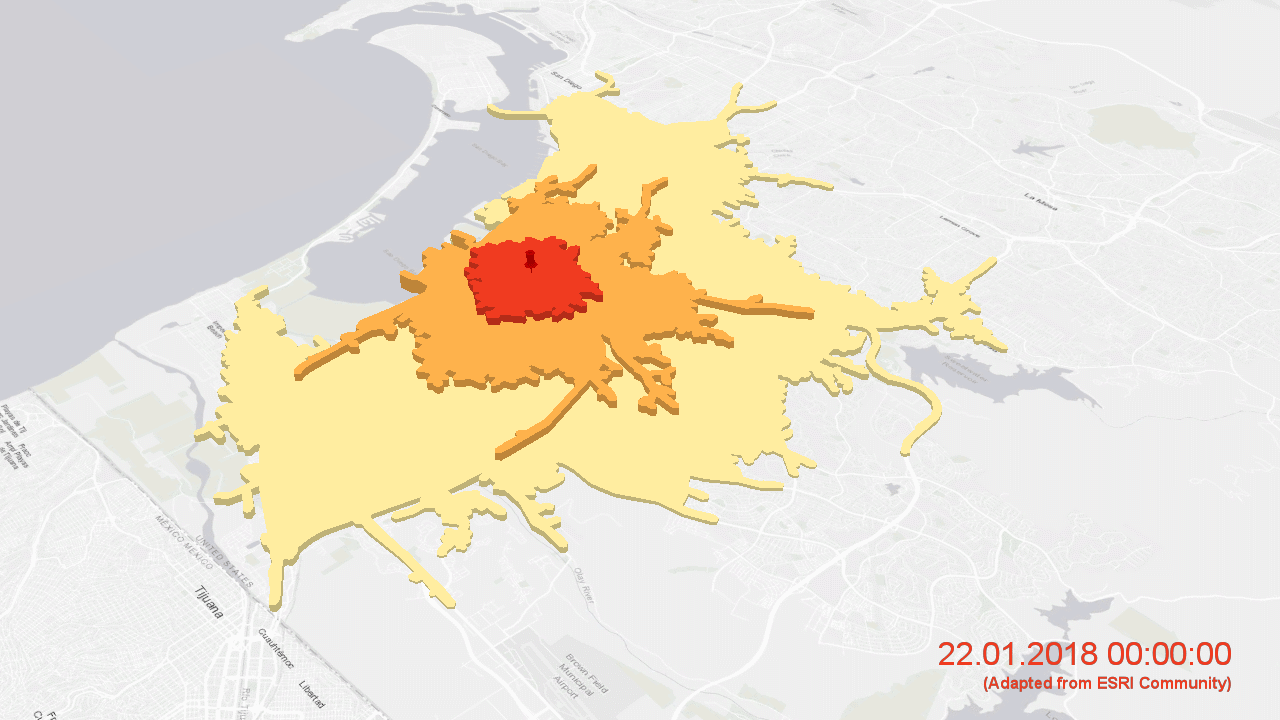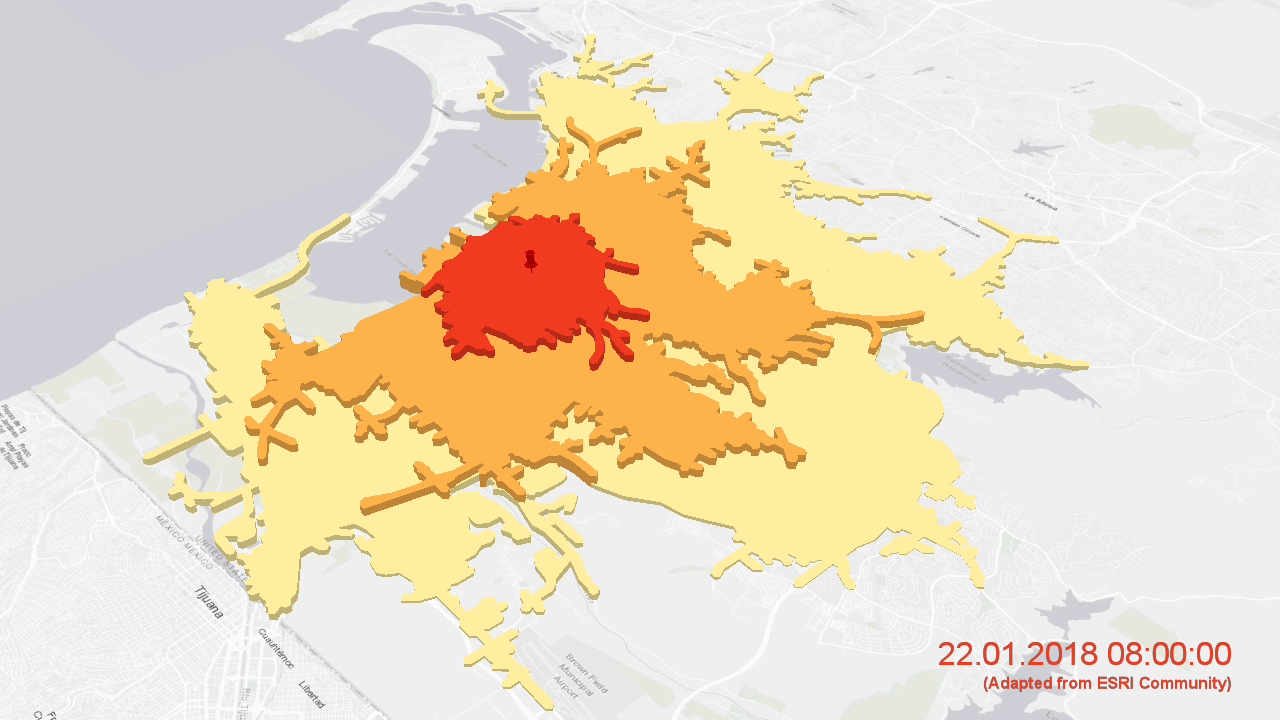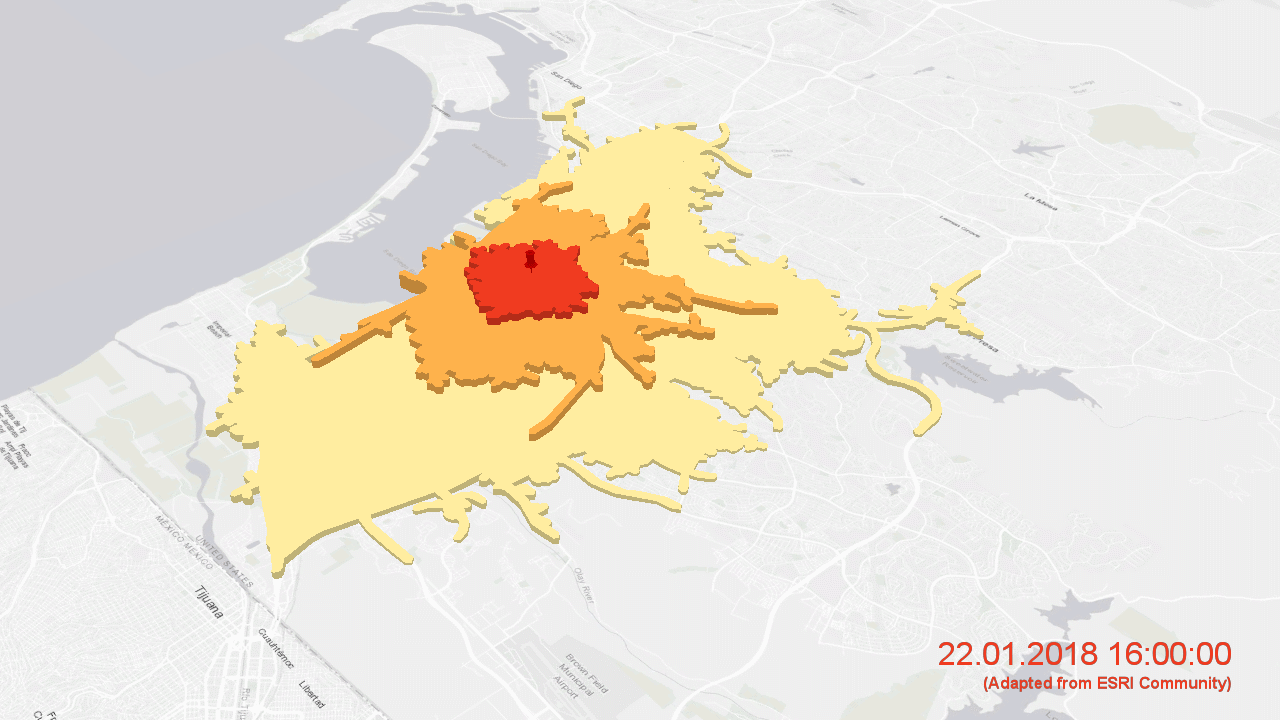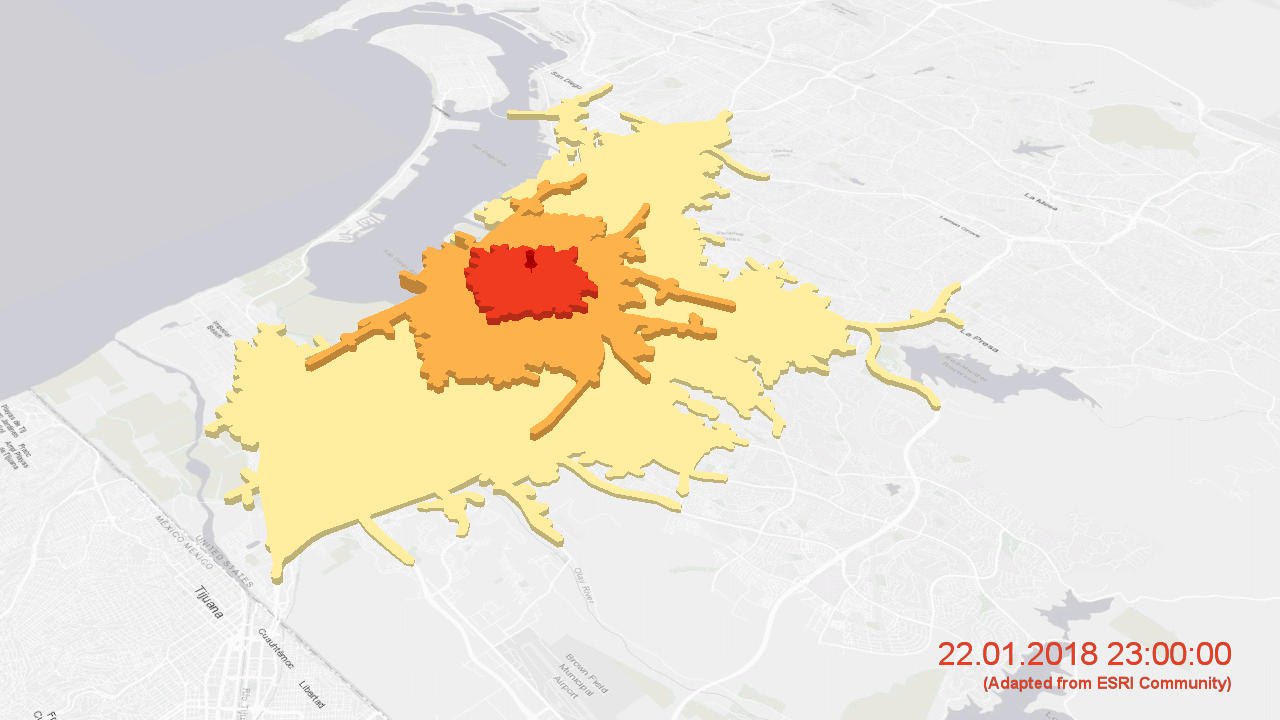
Erreichbarkeiten im Straßennetz von San Diego von einem zentralen Punkt aus in vier, acht und zwölf Minuten für unterschiedliche Tageszeiten (animiert mit ArcGIS Pro unter Einsatz eines ESRI-Straßendatensatzes
- Modelle und Simulationen als komplexe Methoden sind aus den jeweiligen Fachdisziplinen speziell zusammengestellte Abläufe, die bestimmte Phänomene und Verhaltensweisen der realen Welt mathematisch nachbilden. Als Methode bietet sich hierfür z. B. die sogenannte Map Algebra an. Die Lärmausbreitung oder die Schadstoffausbreitung in Gewässer kann z. B. mittels GIS-Unterstützung modelliert und berechnet werden, wobei hier meist eine Kombination großer Simulationsmodelle mit GIS erfolgt. Geodaten werden dem Simulationsmodell zugeführt, die Ergebnisse der Simulation können in Form von Isolinien im GIS visualisiert werden.
